Welcome to the fascinating realm of electrical engineering, where circuits come to life through the intricate dance of components like capacitors. Among the myriad factors influencing circuit behavior, impedance holds a significant place, particularly concerning capacitors.
In this article, we embark on a journey to demystify the concept of impedance of capacitors, exploring its definition, significance, practical implications, and frequently asked questions.
Impedance of Capacitor
The impedance of a capacitor refers to the opposition that a capacitor presents to the flow of alternating current (AC) within an electrical circuit. In simpler terms, it’s the measure of how much the capacitor resists the flow of AC.
This impedance is a combination of resistance and reactance. While resistance limits the current flow in a circuit, reactance arises due to the capacitor’s ability to store and release electrical energy. So, impedance essentially encapsulates both these factors, offering a comprehensive view of how a capacitor interacts with AC within a circuit.
Understanding Impedance
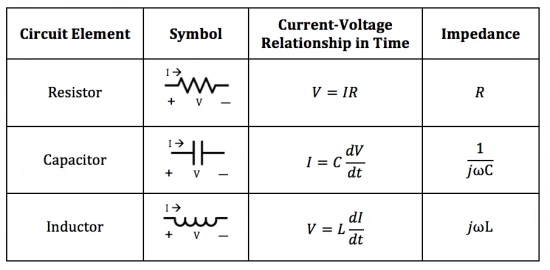
Impedance is a fundamental concept in electrical engineering, representing the total opposition that a circuit offers to the flow of alternating current (AC). It encompasses both resistance, which restricts the flow of current, and reactance, which arises due to the capacitor’s ability to store and release electrical energy. Essentially, impedance provides a holistic view of how a circuit interacts with AC, considering both resistive and reactive elements.
How to Find Impedance of a Capacitor
Finding the impedance of a capacitor involves a straightforward process. Here’s a simplified guide:
- Identify Frequency and Capacitance: Determine the frequency of the alternating current (AC) circuit in hertz (Hz) and the capacitance of the capacitor in farads (F). These values are essential for calculating impedance.
- Use the Impedance Formula: Apply the impedance formula specific to capacitors:𝑍𝑐=12𝜋𝑓𝐶Zc=2πfC1Where:
- 𝑍𝑐Zc represents the impedance of the capacitor (in ohms).
- 𝑓f denotes the frequency of the AC circuit (in Hz).
- 𝐶C stands for the capacitance of the capacitor (in farads).
- Substitute Values: Insert the known values of frequency (𝑓f) and capacitance (𝐶C) into the formula.
- Perform Calculation: Calculate the impedance using the formula. Ensure accuracy in arithmetic operations.
- Interpret Result: The computed value represents the impedance of the capacitor at the specified frequency. It indicates the total opposition offered by the capacitor to the flow of alternating current.
By following these steps, you can effectively determine the impedance of a capacitor, aiding in circuit analysis and design for various electrical applications.
Impedance vs. Resistance
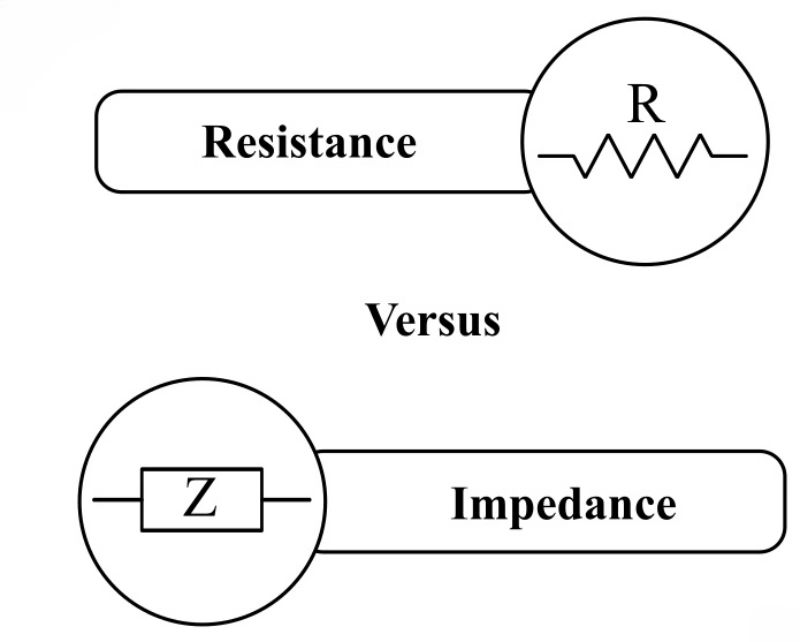
While both impedance and resistance relate to the opposition to current flow in a circuit, they have distinct characteristics and behaviors, particularly in the context of capacitors.
Resistance is a property that restricts the flow of current in a circuit, converting electrical energy into heat. It remains constant regardless of the frequency of the alternating current passing through the circuit. In contrast, impedance encompasses both resistance and reactance. Reactance arises from the capacitor’s ability to store and release electrical energy in response to changes in voltage.
The key difference lies in their response to alternating current frequencies. Resistance remains constant regardless of frequency, while impedance varies with frequency due to the capacitive reactance component. As the frequency increases, the capacitive reactance decreases, allowing more current to flow through the capacitor.
Here’s a table comparing resistance and impedance:
| Property | Resistance | Impedance |
|---|---|---|
| Definition | Opposition to current flow in a circuit | Total opposition to AC flow in a circuit |
| Components | Only resistive component | Resistive and reactive components |
| Symbol | 𝑅R | 𝑍Z |
| Frequency Dependence | Does not vary with frequency | Varies with frequency due to reactance |
| Representation in AC Circuits | Remains constant | Varies with frequency due to capacitive reactance |
This table provides a concise comparison between resistance and impedance, highlighting their key differences and characteristics.
Capacitor Impedance Formula
The impedance of a capacitor in an AC circuit can be calculated using the following formula:
𝑍𝑐=12𝜋𝑓𝐶Zc=2πfC1
Where:
- 𝑍𝑐Zc is the impedance of the capacitor (in ohms).
- 𝑓f is the frequency of the alternating current (in hertz).
- 𝐶C is the capacitance of the capacitor (in farads).
This formula demonstrates that the impedance of a capacitor (𝑍𝑐Zc) is inversely proportional to both the frequency of the alternating current (𝑓f) and the capacitance of the capacitor (𝐶C). As the frequency increases, the impedance decreases, allowing more current to flow through the capacitor. Similarly, as the capacitance increases, the impedance decreases, again allowing more current to flow.
How to Calculate Impedance of a Capacitor
Calculating impedance of a capacitor in an AC circuit involves using a simple formula. Here’s a step-by-step guide:
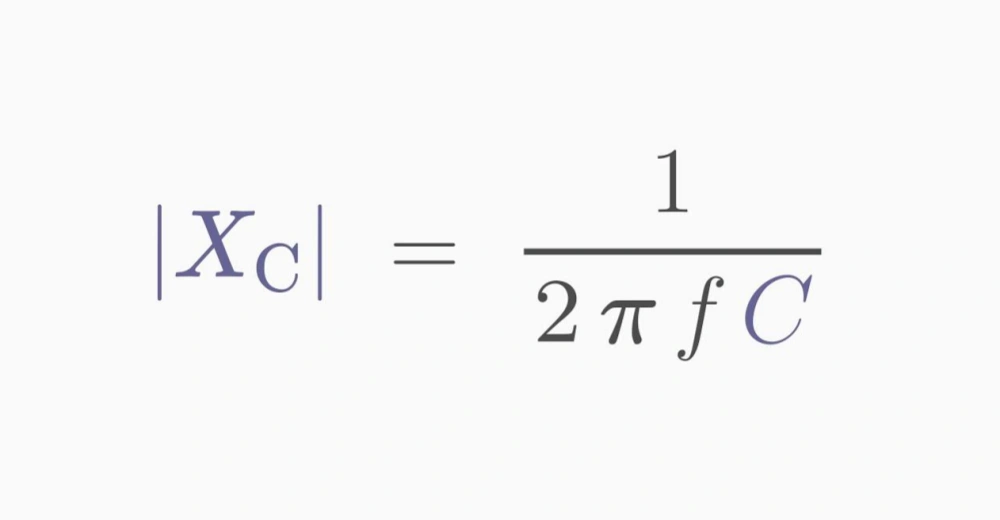
- Gather Information: Obtain the frequency of the alternating current (AC) in hertz (Hz) and the capacitance of the capacitor in farads (F). Ensure these values are accurately measured or provided.
- Use the Impedance Formula: Apply the impedance formula for a capacitor:𝑍𝑐=12𝜋𝑓𝐶Zc=2πfC1Where:
- 𝑍𝑐Zc is the impedance of the capacitor (in ohms).
- 𝑓f is the frequency of the AC (in Hz).
- 𝐶C is the capacitance of the capacitor (in farads).
- Substitute Values: Plug the frequency (𝑓f) and capacitance (𝐶C) values into the formula.
- Calculate: Perform the calculations using the formula.
- Interpret Result: The resulting value will be the impedance of the capacitor in ohms. This impedance represents the total opposition offered by the capacitor to the flow of alternating current at the given frequency.
By following these steps, you can accurately calculate the impedance of a capacitor in an AC circuit, providing valuable insights into its behavior and interaction with the electrical system.
How to Calculate Impedance of Resistor and Capacitor in Parallel
To calculate the impedance of a resistor and capacitor in parallel, you can follow these steps:
- Understand Parallel Impedance: In a parallel circuit, the reciprocal of the total impedance (𝑍totalZtotal) is equal to the sum of the reciprocals of the individual impedances. Mathematically, it can be expressed as:1𝑍total=1𝑍resistor+1𝑍capacitorZtotal1=Zresistor1+Zcapacitor1
- Calculate Resistor Impedance: The impedance of a resistor (𝑍resistorZresistor) is simply the resistance value itself, denoted by 𝑅R. So, 𝑍resistor=𝑅Zresistor=R.
- Calculate Capacitor Impedance: The impedance of a capacitor (𝑍capacitorZcapacitor) in an AC circuit is given by:𝑍capacitor=12𝜋𝑓𝐶Zcapacitor=2πfC1Where:
- 𝑓f is the frequency of the AC circuit (in Hz).
- 𝐶C is the capacitance of the capacitor (in farads).
- Substitute Values: Substitute the resistance value (𝑅R), frequency (𝑓f), and capacitance (𝐶C) into the equations for resistor impedance and capacitor impedance.
- Calculate Parallel Impedance: Use the formula for parallel impedance to find the total impedance (𝑍totalZtotal).
- Interpret Result: The calculated value of 𝑍totalZtotal represents the total impedance of the resistor and capacitor combination in parallel at the specified frequency.
Capacitor Impedance Calculator
Capacitor Impedance Calculator
Upon submitting the form, it calculates the impedance of the capacitor.
Capacitor Impedance vs Frequency Calculator
To calculate the impedance of a capacitor at different frequencies, you can use the following capacitor impedance vs. frequency calculator:
- Frequency Range: Define the range of frequencies for which you want to calculate the impedance.
- Capacitance Value: Input the capacitance value of the capacitor in farads (F).
- Formula: Utilize the impedance formula for capacitors:𝑍𝑐=12𝜋𝑓𝐶Zc=2πfC1Where:
- 𝑍𝑐Zc is the impedance of the capacitor (in ohms).
- 𝑓f is the frequency of the AC circuit (in Hz).
- 𝐶C is the capacitance of the capacitor (in farads).
- Iterative Calculation: Input different frequencies within the defined range and calculate the corresponding impedance values using the formula.
- Tabulate Results: Organize the calculated impedance values corresponding to each frequency in a table for better visualization.
- Graphical Representation (Optional): Plot a graph with frequency on the x-axis and impedance on the y-axis to visualize the relationship between frequency and capacitor impedance.
Here’s a table for a capacitor impedance vs. frequency calculator:
| Frequency (Hz) | Capacitor Impedance (Zc) |
|---|---|
| 𝑓1f1 | 𝑍𝑐1=12𝜋𝑓1𝐶Zc1=2πf1C1 |
| 𝑓2f2 | 𝑍𝑐2=12𝜋𝑓2𝐶Zc2=2πf2C1 |
| 𝑓3f3 | 𝑍𝑐3=12𝜋𝑓3𝐶Zc3=2πf3C1 |
| ⋮⋮ | ⋮⋮ |
| 𝑓𝑛fn | 𝑍𝑐𝑛=12𝜋𝑓𝑛𝐶Zcn=2πfnC1 |
In this table:
- Frequency (Hz): This column represents the frequencies at which you want to calculate the capacitor impedance.
- Capacitor Impedance (Zc): This column shows the formula used to calculate the impedance of the capacitor at each frequency. 𝐶C denotes the capacitance value in farads, and 𝑓𝑖fi represents each frequency within the specified range.
You can input different frequencies (𝑓1,𝑓2,𝑓3,…,𝑓𝑛f1,f2,f3,…,fn) and calculate the corresponding capacitor impedance values (𝑍𝑐1,𝑍𝑐2,𝑍𝑐3,…,𝑍𝑐𝑛Zc1,Zc2,Zc3,…,Zcn) using the given formula for each frequency.
FAQs
How does impedance affect the performance of capacitors?
Impedance influences the flow of alternating current through capacitors, impacting their ability to store and release electrical energy efficiently.
Can impedance of capacitors be ignored in DC circuits?
Yes, in DC circuits, where frequency is constant, impedance reduces to the capacitance’s resistance, making its effect negligible.
What factors affect the capacitive reactance?
The capacitive reactance is inversely proportional to the frequency of the alternating current and directly proportional to the capacitance value.
Why does capacitive reactance decrease with increasing frequency?
As the frequency of alternating current increases, the time available for charge to accumulate and dissipate decreases, leading to a decrease in capacitive reactance.
How does impedance impact power factor correction?
By introducing capacitors in electrical systems, impedance correction reduces reactive power, improving power factor and overall system efficiency.
What role does phase relationship play in capacitive circuits?
The phase shift introduced by capacitive reactance affects the timing of current flow relative to voltage, influencing circuit behavior and performance.
Conclusion
In conclusion, the impedance of capacitors embodies a crucial aspect of electrical circuits, shaping their behavior and performance in diverse applications. By understanding the intricacies of impedance, engineers and enthusiasts alike can unravel the electrical puzzle, harnessing the power of capacitors to drive innovation and efficiency in modern technology.
