A capacitor is a passive electronic component that can store electrical energy in an electric field. It is made up of two conductive plates separated by an insulating material called a dielectric. When a voltage is applied across the plates, it creates an electric field between them.
The amount of energy stored in a capacitor depends on the electric field between the plates and the charge stored on them. The capacitance, measured in farads (F), indicates how much charge the capacitor can store at a given voltage.
How Does a Capacitor Store Energy?
A capacitor is an essential component in electronic circuits, known for its ability to store and release electrical energy. It consists of two conductive plates separated by an insulating material called a dielectric. When a voltage is applied across the plates, an electric field develops across the dielectric, causing a positive charge to accumulate on one plate and a negative charge on the other. This separation of charge creates an electric potential difference between the plates, storing energy in the electric field.
The amount of energy stored in a capacitor depends on the voltage applied and the capacitance of the capacitor, which is determined by the surface area of the plates, the distance between them, and the properties of the dielectric material.
Capacitors can discharge rapidly, making them ideal for applications like camera flashes, power conditioning, and smoothing out electrical noise in circuits. Additionally, capacitors are widely used in power supplies, signal processing, and energy storage systems, highlighting their versatility and importance in modern electronics.
How to Calculate the Energy Stored in a Capacitor?
Calculating the energy stored in a capacitor involves using a simple formula derived from the relationship between voltage, charge, and capacitance. Here’s a step-by-step guide on how to do it:
Formula for Energy Stored in a Capacitor
The energy (E) stored in a capacitor can be calculated using the formula:
- E is the energy in joules (J),
- 𝐶 is the capacitance in farads (F),
- 𝑉 is the voltage across the capacitor in volts (V).
Steps to Calculate the Energy
- Determine the Capacitance (C):
- Identify the capacitance value of the capacitor, which is typically provided in microfarads (µF), nanofarads (nF), or picofarads (pF). If needed, convert this to farads (1 µF = 10^-6 F, 1 nF = 10^-9 F, 1 pF = 10^-12 F).
- Measure or Obtain the Voltage (V):
- Measure the voltage across the capacitor using a voltmeter, or use the voltage value provided by the problem or datasheet.
- Apply the Formula:
- Plug the values of capacitance and voltage into the formula to calculate the energy.
How Do Capacitors and Inductors Store Energy?
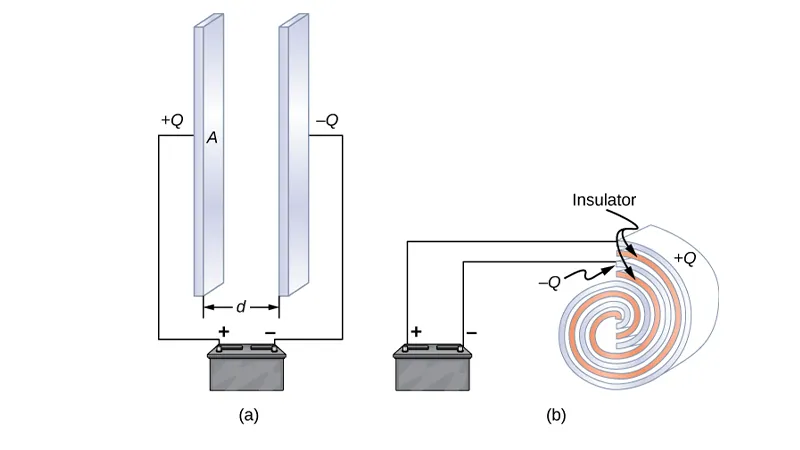
Now that we’ve described how capacitors store energy, let’s explain how inductors store energy.
Structure of an Inductor
An inductor typically consists of a coil of wire, which can be wound around a core made of magnetic material (such as iron) or simply air (air-core inductors).
Mechanism of Energy Storage
- Current Flow and Magnetic Field Generation:
- When an electric current flows through the coil of the inductor, it creates a magnetic field around the coil according to Ampère’s Law.
- The direction of the magnetic field follows the right-hand rule: if you wrap your right hand around the coil with your thumb pointing in the direction of the current, your fingers will curl in the direction of the magnetic field lines.
- Energy Storage in the Magnetic Field:
- The energy is stored in the magnetic field generated by the current flowing through the coil.
- As the current increases, the magnetic field becomes stronger, and more energy is stored.
- Inductive Reactance and Self-Induction:
- Inductors resist changes in current due to their property of inductive reactance.
- If the current through the inductor changes, the changing magnetic field induces a voltage (electromotive force, or EMF) in the coil that opposes the change in current (Lenz’s Law). This self-induction is a key characteristic of inductors.
| Aspect | Capacitors | Inductors |
|---|---|---|
| Form of Energy Storage | Store energy in an electric field created by separated charges | Store energy in a magnetic field created by current flow |
| Energy Dependence | Energy depends on voltage (squared) | Energy depends on current (squared) |
| Behavior in Circuits | Resist changes in voltage. When charging, the voltage gradually increases and then levels off as it approaches the supply voltage. | Resist changes in current. When current through an inductor changes, it induces a voltage opposing the change (Lenz’s Law). |
Different Uses of Capacitors and Inductors
- Capacitors: Used in applications requiring energy storage, smoothing out voltage fluctuations, filtering signals, and timing applications (RC circuits).
- Inductors: Used in applications needing energy storage in a magnetic field, filtering signals in power supplies, tuning circuits (LC circuits), and transformers.
How Do Capacitors Release Energy?

- Initial Conditions:
- Initially, the capacitor is charged and holds a certain amount of electric potential energy due to the separation of charges across its plates.
- Discharge Path:
- When a discharge path is established in the circuit (e.g., by closing a switch), the stored electric charge begins to flow out of the capacitor.
- This discharge path could be a resistor, an inductor, or any other component connected across the capacitor.
- Current Flow:
- As the charge starts flowing, a current is established in the circuit. The rate of discharge depends on the resistance of the discharge path and the capacitance of the capacitor.
- Voltage Decrease:
- As the charge leaves the capacitor, the voltage across its terminals decreases. This decrease in voltage is proportional to the decrease in stored energy.
- Energy Release:
- The electric potential energy stored in the capacitor is gradually released into the circuit in the form of current flow.
- This released energy can perform work in the circuit, such as powering a device or generating a magnetic field in an inductor.
How Long Can a Capacitor Store Energy?
The duration a capacitor can store energy depends on several factors, including the type of capacitor, the quality of its dielectric material, and external conditions like temperature and humidity. Here are the key factors affecting the energy storage duration of a capacitor:
Key Factors Affecting Energy Storage Duration
- Leakage Current: All capacitors have some amount of leakage current, which is the small current that flows across the dielectric even when the capacitor is not connected to a circuit. High-quality capacitors have lower leakage currents, allowing them to store energy for longer periods.
- Dielectric Material: The type and quality of the dielectric material used in the capacitor significantly affect its ability to store energy. Materials with high dielectric strength and low leakage current properties enable longer storage durations.
- Capacitor Type: Different types of capacitors (e.g., electrolytic, ceramic, film, supercapacitors) have varying storage capabilities. For instance, supercapacitors can store energy for extended periods compared to traditional electrolytic capacitors.
- Environmental Conditions: Temperature and humidity can affect the leakage current and overall stability of the capacitor. Higher temperatures typically increase the leakage current, reducing the storage duration. Humidity can also impact the dielectric material, especially in capacitors not sealed properly.
- Aging and Degradation: Over time, capacitors can degrade due to chemical reactions within the dielectric or other internal components. This degradation increases leakage currents and decreases the capacitor’s ability to hold a charge for long periods.
Practical Storage Durations
- Electrolytic Capacitors: These capacitors, commonly used for power supply filtering, can typically hold a charge for several minutes to hours, depending on the leakage current and environmental conditions.
- Ceramic and Film Capacitors: These capacitors have lower leakage currents and can store energy for a longer period, ranging from hours to days.
- Supercapacitors: Supercapacitors, known for their high capacitance values, can store energy for weeks or even months, making them suitable for applications requiring long-term energy storage.
Estimating Storage Duration
While it is challenging to provide an exact storage duration for all capacitors due to the influencing factors, the following general guidelines can help estimate the storage duration:
- Low-Leakage Ceramic or Film Capacitors: Days to weeks.
- Electrolytic Capacitors: Minutes to hours.
- Supercapacitors: Weeks to months.
How Much Energy is Stored in the Capacitor?
Suppose you have a capacitor with a capacitance of 10 µF (microfarads) charged to a voltage of 5 V. The energy stored can be calculated as follows:
Convert Capacitance to Farads: 10 µF=10×10−6 F10µF=10×10−6F
Use the Formula:
E=125µJ
How to Calculate The Energy Density of a Capacitor?
The energy density per unit volume can be calculated using the formula:
- u is the energy density in joules per cubic meter (J/m³),
- 𝐸 is the energy stored in joules (J),
- 𝑉cap is the volume of the capacitor in cubic meters (m³).
Steps to Calculate Energy Density Per Unit Volume
- Calculate the Energy Stored: Use the formula 𝐸=1/2×𝐶𝑉² to find the energy stored in the capacitor.
- Determine the Volume of the Capacitor: Measure or obtain the volume 𝑉capVcap of the capacitor. This can be calculated if you know the dimensions of the capacitor.
- Calculate the Energy Density: Divide the energy stored 𝐸 by the volume 𝑉cap.
Example Calculation
Suppose you have a capacitor with a capacitance of 10 µF (microfarads) charged to a voltage of 100 V, and the volume of the capacitor is 1×10−61×10−6 m³.
- Convert Capacitance to Farads: 10 µF=10×10−6 F10µF=10×10−6F
- Calculate the Energy Stored:𝐸=1/2×𝐶𝑉²=1/2×10×10−6F×(100V)²=0.05J
- Calculate the Energy Density:u=E/Vcap=0.05/1×10^-6=5×10^4 J/m^3
Conclusion
The capacitor is a passive electronic component capable of storing electrical energy in an electric field. It comprises two conductive plates separated by an insulating material called a dielectric
Applying voltage across the plates generates an electric field, causing positive charge to accumulate on one plate and negative charge on the other.
The stored energy depends on the applied voltage and capacitance, the latter determined by plate surface area, spacing, and dielectric properties. Capacitors discharge rapidly, making them suitable for applications like camera flashes, power conditioning, and circuit noise reduction.




















