The Capacitor Time Constant is a crucial concept in electronics that influences how capacitors charge and discharge. It defines the time it takes for a capacitor to reach about 63% of its full voltage. Understanding this time constant helps you design better circuits and troubleshoot problems more efficiently.
Dive deeper into the Capacitor Time Constant and enhance your tech knowledge. Don’t miss out—read on to discover its full impact!
What Is Capacitor Time Constant?
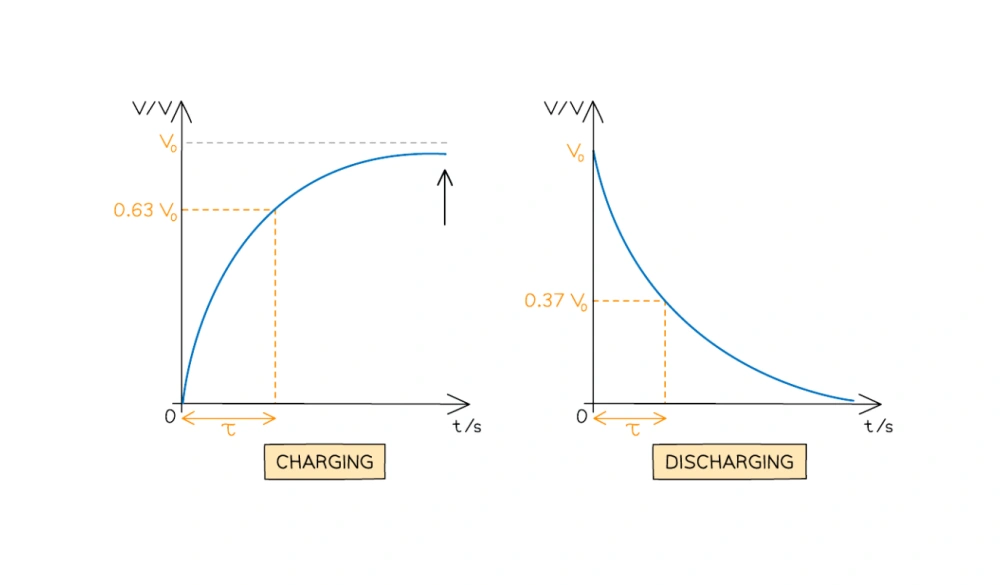
Capacitor Time Constant Definition: The Capacitor Time Constant is a measure of how fast a capacitor charges or discharges in an electrical circuit. It indicates the time required for the capacitor’s voltage to reach approximately 63% of its final value. This constant plays a crucial role in understanding the behavior of capacitors in various electronic applications.
Capacitor Time Constant Formula: The formula for the Capacitor Time Constant is τ = R × C, where τ (tau) represents the time constant, R is the resistance in ohms, and C is the capacitance in farads. This simple yet powerful equation helps you calculate the time it takes for a capacitor to charge or discharge in an RC circuit.
Importance: The Capacitor Time Constant is vital for designing circuits with precise timing, such as filters and oscillators. It directly influences how quickly a capacitor responds to voltage changes, affecting the overall performance and stability of electronic devices. Understanding this constant allows engineers to optimize circuits for speed and efficiency.
How The Time Constant Works?
The significance of the time constant in capacitor charging and discharging: The Capacitor Time Constant (τ) is a key factor in determining how quickly a capacitor charges and discharges in an RC circuit. It defines the rate at which a capacitor’s voltage increases or decreases when connected to a power source or a load.
The higher the time constant, the slower the capacitor responds, and vice versa. This behavior directly impacts how efficiently circuits perform, especially in timing and filtering applications.
What 63% charging means: When a capacitor begins charging, the Capacitor Time Constant tells us that after one time constant (τ), the capacitor will reach approximately 63% of its final voltage. This means it’s not fully charged but has made significant progress.
For engineers, this provides a predictable way to gauge how much charge has been accumulated over time, helping in the design of circuits that require specific charging times.
Full charge or discharge after 5 time constants: After 5 time constants, a capacitor is considered nearly fully charged or discharged, reaching over 99% of its total voltage. This means that the capacitor’s behavior stabilizes after 5 τ, and very little change occurs beyond this point.
Understanding this allows designers to fine-tune circuits to achieve their desired performance, knowing that after this threshold, the capacitor is effectively at its maximum charge or discharge.
Impact of R and C on Time Constant
How increasing resistance (R) affects the time constant: Increasing the resistance (R) in an RC circuit directly increases the Capacitor Time Constant. With higher resistance, the capacitor charges and discharges more slowly. This is because the resistance limits the flow of current, forcing the capacitor to take more time to reach its final voltage. Slower charging or discharging is beneficial for circuits that require precise timing.
How increasing capacitance (C) affects the time constant: Increasing capacitance (C) also increases the Capacitor Time Constant. A larger capacitance means the capacitor can store more charge, which results in a slower voltage change. As the capacitor needs more time to accumulate or release this larger amount of charge, the overall charging and discharging time increases significantly.
Real-life examples of both effects: In real-life applications, increasing resistance might be used in filters to slow down the response time for smoother signal processing. On the other hand, increasing capacitance could be seen in power supply circuits, where larger capacitors help stabilize voltage levels. Both changes in R and C modify the Capacitor Time Constant, giving engineers more control over circuit behavior.
Calculate Capacitor Time Constant
Step-by-step Procedure For Calculation
Identify the resistance value (R): Start by identifying the resistance (R) in your circuit. This is typically measured in ohms (Ω) and controls the rate at which current flows through the capacitor. The resistance determines how quickly the capacitor charges or discharges, making it a key factor in calculating the Capacitor Time Constant (τ).
Identify the capacitance value (C): Next, find the capacitance (C), which is measured in farads (F). The capacitance indicates how much charge the capacitor can store. A higher capacitance means the capacitor can hold more charge, influencing how long it takes to reach a certain voltage during the charge and discharge cycles.
Apply the formula τ = R × C: Once you have the resistance and capacitance values, use the formula τ = R × C to calculate the time constant. This equation gives you the time it takes for the capacitor to charge up to about 63% of its total voltage or discharge to about 37% of its initial voltage. The larger the time constant, the slower the charge and discharge process.
Example calculations with specific values for R and C: For instance, if the resistance is 1,000 ohms (1kΩ) and the capacitance is 0.01 farads (10,000µF), you can calculate the Capacitor Time Constant (τ) by multiplying 1,000 × 0.01. This results in τ = 10 seconds. This means the capacitor will take 10 seconds to charge or discharge by about 63% of its total voltage.
Charging And Discharging Of Capacitor Time Constant
Capacitor Charge Time Constant: The capacitor charge time constant refers to how quickly a capacitor charges through the resistor in a circuit. It takes about one capacitor time constant (τ) for the capacitor to reach 63% of its maximum voltage.
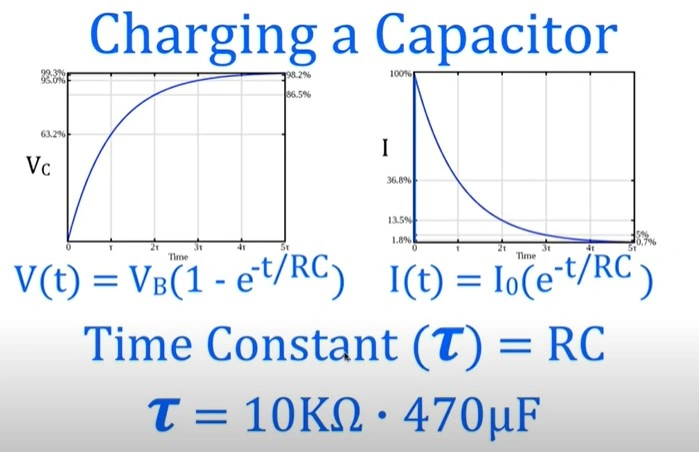
After five time constants, the capacitor is almost fully charged, at 99%. The larger the time constant, the slower the capacitor charges, making it crucial for designing circuits that require specific charge rates.
Capacitor Discharge Time Constant: The capacitor discharge time constant governs how quickly the capacitor loses its stored charge. Similarly, after one capacitor time constant (τ), the capacitor will have discharged to about 37% of its initial voltage.
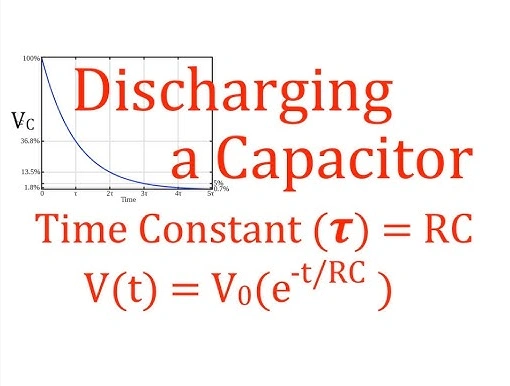
The capacitor continues to discharge exponentially, reaching near-zero voltage after five time constants. The discharge rate also depends on the resistance and capacitance values in the circuit.
How Many Time Constants for a Capacitor to Fully Charge?
To fully charge a capacitor, it typically takes 5 Capacitor Time Constants (τ). After one time constant, the capacitor reaches about 63% of its full voltage. At two time constants, it reaches around 86%, and by the time it hits 5 time constants, the capacitor is almost completely charged, reaching 99%.
Understanding the Capacitor Time Constant helps you predict how quickly a capacitor will charge or discharge in various circuits, allowing for better circuit design and optimization.
How Many Time Constants For A Capacitor To Fully Discharge?
A capacitor takes about five Capacitor Time Constants (τ) to fully discharge. After one time constant, the capacitor has discharged to about 37% of its initial voltage. By the time it reaches five time constants, the voltage drops to nearly zero—specifically, only about 0.7% remains.
The larger the time constant, the slower the discharge process, making this important for designing circuits where precise discharge rates are necessary.
Capacitor Time Constant Practical Applications
Filtering Circuits: The Capacitor Time Constant is crucial in filtering circuits, where it determines how quickly a signal is smoothed or filtered. In low-pass filters, for example, a larger time constant allows low-frequency signals to pass through while blocking high-frequency noise. Engineers adjust the time constant to fine-tune filter performance and ensure clear signal transmission.
Timing and Signal Processing: The Capacitor Time Constant plays a key role in timing circuits and signal processing. It controls the rate at which capacitors charge or discharge, making it essential in creating precise delays or oscillations. In oscillators and pulse circuits, this constant helps define the timing intervals, ensuring accurate and reliable operation for various applications, like clocks or waveform generators.
Power Supplies and Audio Systems: In power supplies, the Capacitor Time Constant helps regulate voltage by controlling how quickly capacitors charge during the rectification process. Similarly, in audio systems, capacitors with a well-calculated time constant smooth out voltage fluctuations, ensuring consistent sound quality.
These applications rely on precise capacitor behavior to maintain stability and performance in electronics.
Conclusion
In conclusion, the Capacitor Time Constant is a fundamental concept that affects how capacitors charge and discharge in circuits. It influences everything from filtering and timing to signal processing and power regulation.
Understanding this time constant empowers engineers to design more efficient, stable, and precise circuits. Ready to dive deeper? Quote a Capacitor from Weishi today and take your projects to the next level!
FAQ
What is the RC time constant of a capacitor?
The RC time constant (τ) of a capacitor is the time it takes for the capacitor to charge to approximately 63.2% of its full voltage or discharge to 36.8% of its initial voltage. It is determined by the product of the resistance (R) and capacitance (C) values in the circuit, represented by the formula τ = R × C.
Why is the time constant 63.2%?
The 63.2% value comes from the natural logarithmic behavior of a capacitor’s charge or discharge. After one time constant, the voltage across the capacitor reaches 63.2% of its maximum value during charging or drops to 36.8% during discharging. This percentage represents approximately 1 – (1/e), where e is Euler’s number, a constant in mathematics.
What is the time factor of a capacitor?
The time factor of a capacitor typically refers to the time constant (τ), which defines the rate at which the capacitor charges or discharges. The time factor determines how quickly a capacitor reaches a significant portion (63.2%) of its maximum voltage during charging or drops to 36.8% during discharging. The time factor depends on the resistance and capacitance in the circuit.
How do you calculate tau?
To calculate τ (tau), simply multiply the resistance (R) in ohms (Ω) by the capacitance (C) in farads (F). The formula is τ = R × C. The result gives you the time constant in seconds, representing the time it takes for the capacitor to charge or discharge by about 63.2% of its total voltage change.