Capacitor Impedance Calculator
If you know the capacitance value (C) of the capacitor and the frequency of the signal passing through it (f), our capacitive reactance calculator can help you determine the impedance of the capacitor.
Enter the capacitance value (in microfarads, μF) and frequency (in Hz) to calculate the impedance.
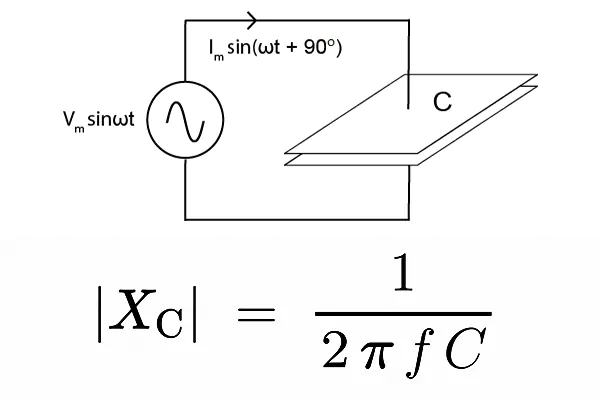
What is Capacitor Impedance?
Capacitor impedance is a measure of the opposition that a capacitor provides to the flow of alternating current (AC) in a circuit. Unlike resistance, which remains constant regardless of frequency, impedance in capacitors varies inversely with the frequency of the AC signal and the capacitance value.
The formula for calculating capacitor impedance is:
Xc=1/2πfC
Where:
- fff is the frequency of the AC signal in Hertz (Hz), and
- CCC is the capacitance in Farads (F).
At higher frequencies, the impedance of a capacitor decreases because the capacitor charges and discharges more quickly, offering less opposition to current flow. Conversely, at lower frequencies, impedance increases significantly, making capacitors effective for blocking low-frequency signals while allowing high-frequency signals to pass.
Capacitor impedance is critical in designing circuits such as filters, oscillators, and frequency selectors. For example, in audio systems, capacitors with specific impedance values are used to separate high, mid, and low frequencies for better sound quality.
Understanding capacitor impedance is essential for optimizing circuit performance, particularly in applications where precise frequency control and signal filtering are required.
Capacitor Impedance in Applications
Power Systems: Managing Reactive Power
In power systems, capacitors are widely used for power factor correction and managing reactive power. Impedance plays a key role in determining how capacitors interact with inductive loads such as transformers and motors. By properly calculating the impedance of capacitors, engineers can optimize the power delivery, reduce energy losses, and ensure stable voltage levels in electrical grids. This reduces the strain on generators and improves system efficiency.
Audio Equipment: Frequency Filters and Equalizers
In audio systems, capacitors are critical for designing filters that separate or emphasize specific frequency ranges. For example, capacitors with calculated impedance values are used in crossovers to divide audio signals into low, mid, and high frequencies, directing them to the appropriate speakers. This ensures clarity and fidelity in sound reproduction. Similarly, equalizers use capacitors to adjust the impedance for selective boosting or cutting of frequencies, tailoring the audio output to the desired profile.
Signal Processing: Bandwidth Control
In communication circuits, controlling signal bandwidth is essential to transmit data effectively. Capacitor impedance is used to filter out unwanted frequencies, allowing only the desired signals to pass. This is especially important in radio frequency (RF) circuits, where capacitors with precise impedance values ensure signal clarity and reduce noise. For instance, in wireless communication, impedance matching with capacitors improves antenna performance and minimizes signal loss.
Other Applications
- Power Electronics: Capacitors regulate voltage and filter noise in rectifiers and inverters.
- Automotive Systems: Impedance control in capacitors is used for signal conditioning in vehicle electronics.
- Medical Equipment: Precision in capacitor impedance ensures the accuracy of sensitive diagnostic tools like ECGs.
FAQs
A: Capacitor impedance is inversely proportional to frequency, which means it decreases as the frequency of the AC signal increases. This behavior is due to the relationship:
Zc=1/2πfC
Where "f" is the frequency in Hertz, and "C" is the capacitance in Farads.
At low frequencies, capacitors offer high impedance, effectively blocking the current. Conversely, at higher frequencies, the impedance drops, allowing current to flow more freely. This property makes capacitors essential in frequency-dependent applications like filters and signal processors.
For example:
- At 50 Hz with a 10 μF capacitor, the impedance is approximately 318 Ω.
- At 500 Hz, the impedance decreases to about 31.8 Ω.
Our capacitor impedance vs frequency calculator allows you to input your specific values, plot the relationship, and visualize how impedance changes across various frequencies.
Calculating the impedance of a parallel resistor-capacitor (RC) circuit involves combining the resistance (R) and capacitive reactance (Xc) using the following formula:
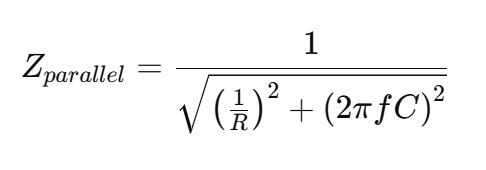
- Calculate Capacitive Reactance(Xc): Determine Xc = 1/2πfC
- Determine Total Impedance: Use the formula to calculate Z parallel, combining the resistance and capacitive reactance.
Parallel RC circuits are used in applications like audio equalizers and signal filters, where accurate impedance calculation is critical for performance. Our capacitor resistor parallel impedance calculator simplifies these calculations by providing instant results for your input values.
Impedance is a fundamental property in AC circuits, representing the total opposition to current flow, combining resistance and reactance. Its importance lies in the following:
- Current Flow Control: Impedance determines how much current flows through a circuit for a given voltage.
- Voltage Distribution: It affects how voltage is divided across circuit components, crucial in designing circuits like voltage dividers.
- Frequency Response: Impedance varies with frequency, enabling selective filtering in audio, communication, and RF systems.
For instance, in power systems, capacitors with calculated impedance are used to correct the power factor, reducing energy losses. In signal processing, impedance ensures efficient energy transfer and minimizes signal distortion.