The Capacitance of Parallel Plate Capacitor is a core concept in electronics, shaping how we understand charge storage and electric fields. Knowing this helps you dive deeper into circuits, enabling you to predict energy flow and optimize designs.
In this guide, we’ll break down the basics and calculations step by step, covering everything from the defining formula to the factors that influence capacitance. Ready to master the Capacitance of Parallel Plate Capacitor? Let’s get started!
What Is A Parallel Plate Capacitor?
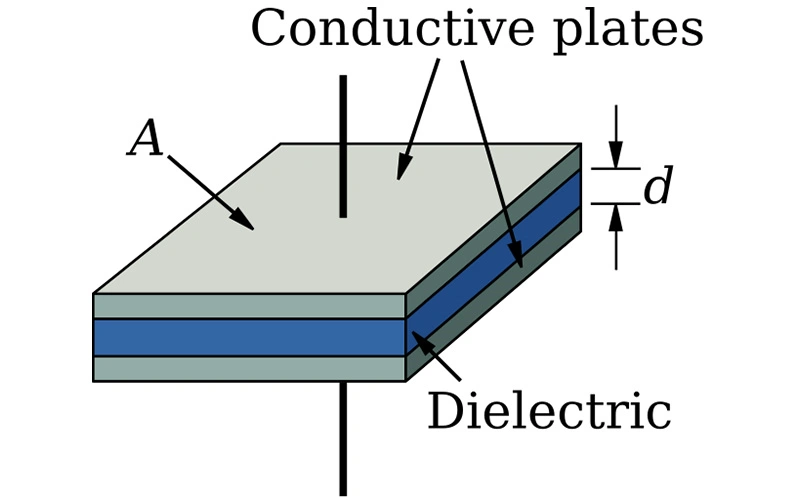
A parallel plate capacitor is a basic yet powerful tool in electronics. It consists of two flat, conductive plates facing each other, separated by an insulating material called a dielectric. When connected to a voltage source, the plates store electric charge, creating an electric field between them.
This setup makes parallel plate capacitors ideal for energy storage, signal filtering, and circuit timing. Their design enhances efficiency by increasing the plate area or decreasing the distance between plates, making them powerful and essential components in various tech applications.
What Is Capacitance Of Parallel Plate Capacitor?
The capacitance of a parallel plate capacitordefines how much electric charge it can store for a given voltage. This value depends on three factors: the area of the plates, the distance between them, and the dielectric material between them.
Larger plates and closer spacing increase the capacitance, making it a powerful way to manage energy storage in circuits. By adjusting these elements, the capacitance of a parallel plate capacitor can be tuned to meet precise tech needs in filtering, timing, and more.
Expression for the Capacitance of a Parallel Plate Capacitor
The capacitance (C) of a parallel plate capacitor is given by the formula:
C = ε₀ * A / d
Where:
- ε₀ is the permittivity of free space, a constant approximately equal to 8.85 × 10⁻¹² F/m.
- A is the area of overlap between the two plates.
- d is the distance between the two plates.
This formula tells us that the capacitance of a parallel plate capacitor is directly proportional to the area of the plates and inversely proportional to the distance between them.
In simpler terms, a larger plate area and a smaller distance between the plates will result in a higher capacitance.
How to Calculate Capacitance of a Parallel Plate Capacitor
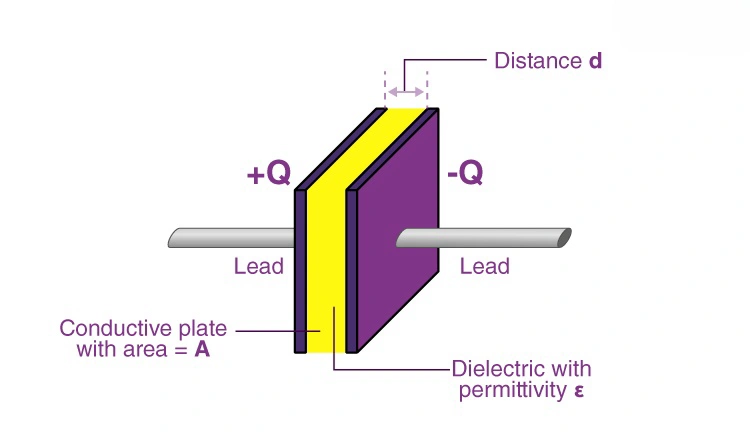
Capacitance of Parallel Plate Capacitor Formula
The capacitance of a parallel plate capacitor depends on the area of the plates, the distance between them, and the dielectric material. Using the formula, you can quickly determine the capacitor’s ability to store electric charge. Here’s the formula:
C=kϵo A/d
where:
- C = Capacitance (in Farads, F)
- ϵ0 = Permittivity of free space (8.85 x 10^-12 F/m)
- ϵr = Relative permittivity (dielectric constant)
- A = Area of one plate (in square meters, m²)
- d = Distance between the plates (in meters, m)
Using this formula, you can see that larger plate area or higher dielectric constant increases capacitance, while a smaller distance between plates also boosts it. Let’s break it down in a table for clarity:
| Parameter | Symbol | Value/Unit |
|---|---|---|
| Capacitance | C | Farads (F) |
| Permittivity of Free Space | ϵ0 | 8.85×10−12F/m |
| Dielectric Constant | ϵr | Unitless (depends on material) |
| Plate Area | A | Square meters (m²) |
| Distance | d | Meters (m) |
Example:
Suppose a capacitor has the following values:
- Plate area A=0.02 m²
- Distance d = 0.001 m
- Dielectric constant ϵr = 2.5
Using the formula:
C=4.43×10−10F
This result tells you the charge storage capacity for this specific parallel plate capacitor.
Derivation of Capacitance of Parallel Plate Capacitor
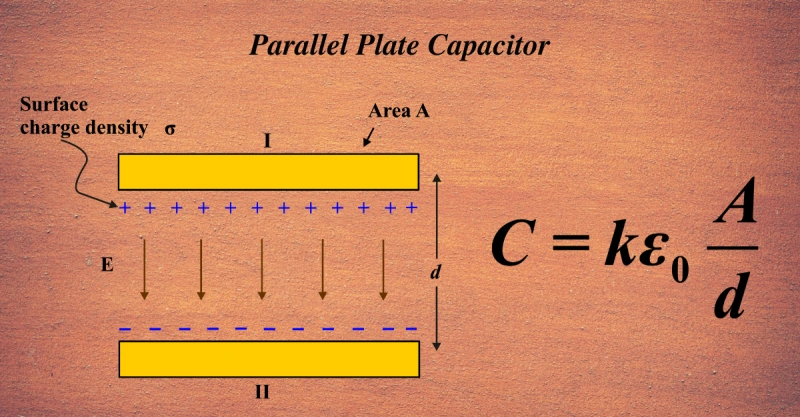
The capacitance of a parallel plate capacitor depends on the plate area, distance between them, and the dielectric between the plates. To derive it, start with the basic capacitor formula: C = Q/V . Here, C is capacitance, Q is charge, and V is voltage.
Using Gauss’s law, you get the electric field E = Q/ϵ0A, where A is plate area, and ϵ0 is the permittivity of free space. Voltage V across the plates equals E × d, where d is the distance between plates. Substituting gives C = ϵ0A/d . This simple formula reveals that increasing plate area boosts capacitance, while increasing distance decreases it—powerful insight for capacitor design.
Factors Affecting Capacitance of A Parallel Plate Capacitor
Plate Area (A): Increasing the plate area gives the capacitor more space to store charge, raising its capacitance. Think of it as expanding a storage unit—more area means more room for charge. Larger plate area creates a powerful way to boost a capacitor’s energy storage potential, making it ideal for high-capacitance needs.
Distance Between Plates: Bringing the plates closer together enhances capacitance. When the distance between plates decreases, the electric field strength rises, allowing more charge to build up. Reducing the gap becomes a powerful tool for maximizing capacitance without changing the plate size or material.
Dielectric Material: The material placed between the plates, called the dielectric, greatly affects capacitance. A high-quality dielectric increases the charge the capacitor can hold. By choosing powerful dielectric materials, like ceramics or polymers, capacitance improves significantly, making capacitors more efficient and reliable.
Dielectric Constant: Different dielectric materials have different constants, directly affecting capacitance. A higher dielectric constant increases a capacitor’s charge capacity. Engineers use powerful dielectrics with high constants to design capacitors with the exact energy storage they need for various applications.
Temperature: Changes in temperature impact capacitance. Most dielectrics expand or contract with temperature shifts, affecting plate spacing and dielectric properties. Consistent temperature control helps maintain capacitance levels, making it a powerful factor in applications sensitive to environmental changes.
Plate Shape: Capacitance can vary slightly with plate shape. Although traditional capacitors use flat plates, altering shapes like curved or patterned surfaces affects electric field distribution, slightly changing capacitance. Exploring different plate shapes offers a powerful approach to optimize capacitor performance for specific designs.
How To Increase Capacitance Of Parallel Plate Capacitor?
To increase the capacitance of a parallel plate capacitor, increase the plate area for greater charge storage. Decrease the distance between plates to intensify the electric field. Choose a dielectric material with a high dielectric constant to store more charge.
Lower temperatures can improve both stability and capacitance. Opt for efficient plate shapes, such as circular or square, to enhance the electric field and optimize performance. Adjusting these factors will maximize capacitor efficiency.
Predict The Change In Capacitance Of A Parallel Plate Capacitor
To predict the change in the capacitance of a parallel plate capacitor, focus on three main factors: plate area, plate distance, and the dielectric material. Increasing the plate area directly boosts the capacitance by allowing more charge storage. Reducing the distance between plates strengthens the electric field, which also raises capacitance.
Lastly, choosing a dielectric with a higher dielectric constant amplifies the charge-holding capacity. Together, these adjustments make predicting the change in the capacitance of a parallel plate capacitor straightforward and effective for fine-tuning performance.
Conclusion
In summary, understanding the Capacitance of Parallel Plate Capacitor is essential for designing efficient circuits. This capacitor’s capacitance depends on the area of the plates, the distance between them, and the dielectric material.
By adjusting these factors, you can optimize the capacitor for better energy storage and stability in various applications. Whether you’re enhancing a circuit or building new tech, choosing the right capacitor is key. Ready to take the next step?
Quote your capacitor from us today and power up your projects!
FAQ
How to calculate the capacitance of a parallel plate capacitor with dielectric?
The capacitance C of a parallel plate capacitor with a dielectric material is calculated using the formula:C=κ⋅ε0⋅A/d. where κ is the dielectric constant,ε0 is the permittivity of free space,A is the area of one plate, and d is the distance between the plates.The dielectric increases the capacitance by reducing the electric field strength.
How to calculate the capacitance of a parallel plate capacitor with a dielectric slab?
If a dielectric slab partially fills the gap between the plates, the capacitor can be divided into two regions: one with the dielectric and one with air. Calculate each region’s capacitance separately, and then use the series or parallel formulas to find the total capacitance based on the slab’s position.
What is the resultant capacitance of a parallel plate capacitor?
For a standard parallel plate capacitor without a dielectric, the capacitance is calculated as: C=ε0⋅A/d
What is the rule for a parallel plate capacitor?
A parallel plate capacitor’s capacitance depends on the plate area, plate separation, and the dielectric material. Capacitance increases with larger plate area or smaller plate distance. Adding a dielectric material between plates increases capacitance by reducing the effective electric field.
Is capacitance constant for a parallel plate capacitor?
Capacitance is constant for a given parallel plate capacitor as long as the plate area, distance between plates, and dielectric properties remain unchanged. Altering any of these factors changes the capacitance, such as increasing capacitance by adding a dielectric.
What happens to the capacitance of a parallel plate capacitor?
The capacitance of a parallel plate capacitor depends on plate area, distance between plates, and the dielectric. Increasing plate area or using a dielectric material increases capacitance, while increasing the distance between plates decreases it. Adding a dielectric can significantly boost capacitance by reducing the effective electric field.
Why do we use parallel plate capacitors?
Parallel plate capacitors are widely used due to their simple structure and the ability to create a uniform electric field between the plates. This uniform field allows for precise calculations and control of capacitance, making them ideal for various applications in electronics and electrical engineering. Additionally, their construction allows for easy adjustment of capacitance by varying the plate area, separation distance, or the type of dielectric material used between the plates. This versatility makes them adaptable to a wide range of circuit designs.
